Kirjoittajat: Hilma Halme & Minna Hannula-Sormunen, Turun yliopisto
Growing Mind –projektin matematiikan osatutkimukset keskittyvät joustavan matemaattisen ajattelun kehitykseen ja tukemiseen (lue myös Uusia välineitä joustavan matemaattisen ajattelun tukemiseen). Joustavalla matemaattisella ajattelulla tarkoitamme oppilaiden kykyä käyttää monipuolisia ratkaisutapoja sekä aiemmin opittua matemaattista tietoa uudenlaisissa tehtävissä ja tilanteissa. Ajattelutaidot ja oppimismotivaatio -tutkimuksessa mittasimme murtolukuosaamisen osa-alueita, joiden on todettu olevan tärkeitä 5. ja 6. luokkalaisten matematiikan osaamisen sekä taitojen kehityksen kannalta. Nämä osa-alueet ovat spontaani huomion kiinnittäminen määrällisiin suhteisiin (SFOR), aritmeettiset taidot kokonais- ja murtoluvuilla, sekä joustava rationaalilukukäsite. Tässä tutkimuksessa mittasimme murtolukuihin liittyvää joustavaa matemaattista ajattelua sekä SFOR-tehtävällä että joustavalla rationaalilukukäsitetehtävällä. Tutkimuksessa mittasimme myös yleistä matematiikka-ahdistusta ja tehtäväkohtaista matematiikka-ahdistusta, eli miten ahdistuneita oppilaat olivat tehtävää tehdessään.
SFOR-tehtävä mittaa oppilaiden taitoja havaita ja sanallistaa matemaattisia suhteita erilaisista kuvista. Esimerkiksi Kuvaa 1 voisi kuvailla siten, että kolmasosa omenoista on punaisia, tai siten, että vihreitä omenoita on kaksi kertaa enemmän kuin punaisia. Koska oppilaille ei kerrottu tehtävän liittyvän matematiikkaan, eikä tutkimusta suoritettu matematiikan tunnilla, voitiin matemaattisten piirteiden havaitsemista kuvista kutsua spontaaniksi eli oma-aloitteiseksi. Spontaani huomion kiinnittäminen matemaattisiin piirteisiin ennustaa murtolukuosaamisen kehitystä (McMullen et al., 2014), sekä liittyy oppilaiden taitoon käyttää koulussa opittuja matemaattisia taitoja arjen tilanteissa. Vain 38% oppilaista huomasi matemaattisia suhteita kuvissa. Onneksi oppilaiden huomion kiinnittämistä määrällisiin suhteisiin on kuitenkin mahdollista vahvistaa, kuten aiempi interventiotutkimuksemme osoitti (Määttä et al., 2022).

Murtoluvut ovat vaikeita monille oppilaille
Oppilailla oli kehitettävää erityisesti murtolukuosaamisessa, sillä yli kolmannes oppilaista ei esimerkiksi vastannut oikein laskuun ”1/3 + 1/3 = ?”. Tämä oli yleisempää oppilaille, jotka eivät olleet käyneet läpi kyseisen lukuvuoden murtolukujaksoa ennen lokakuun ensimmäistä mittauskertaa. Yksi yleisimmistä vastauksista oli 2/6, jossa oppilaat ovat laskeneet murtoluvut yhteen hyödyntäen virheellistä kokonaislukujen laskustrategiaa (1+1= 2 ja 3+3=6). Tämä on yleinen virhekäsitys murtolukujen yhteenlaskusta (Braithwaite et al., 2019; Van Hoof et al., 2015). Murtolukujen opiskeleminen auttoi monia oppilaita pääsemään yli tästä virhekäsityksestä. Kaikkia se ei kuitenkaan auttanut, sillä noin kuudesosalla oppilaista oli tämä virhekäsitys vielä lukuvuoden lopussa tehdyssä mittauksessa. Varsinkin matematiikka-ahdistusta kokevien oppilaiden voi olla vaikea hahmottaa murtolukuja ja sisäistää murtolukuihin liittyviä laskusääntöjä. Matematiikka-ahdistuksen on todettu liittyvän matematiikan välttelemiseen ja kuormittavan oppilaita varsinkin vaikeiden matemaattisten tehtävien suorittamisen aikana, niin että he eivät kykene miettimään selkeästi (Dowker et al., 2016). Murtolukujen yhdistäminen jokapäiväiseen elämään ja murtolukujen havainnoiminen ympäristöstä voisi olla yksi tapa tukea oppilaiden heikkoa murtolukujen hallintaa.

Spontaani huomion kiinnittäminen määrällisiin suhteisiin ennustaa myös joustavaa rationaalilukuosaamista (McMullen et al., 2022), eli oppilaiden taitoa käyttää oppimiaan murtolukukäsitteitä uudenlaisessa tehtävässä. Joustavassa rationaalilukukäsitetehtävässä mitattiin oppilaiden taitoa rakentaa lausekkeita annetuista murto-, desimaali- ja kokonaisluvuista esimerkiksi siten, että tulokseksi muodostui tietty luku. Oppilaat saivat käyttää kaikkia lukuja ja operaattoreita niin monta kertaa kuin halusivat. Tehtävänä oli muodostaa mahdollisimman monta lauseketta kahdessa minuutissa. Suurin osa oppilaista osasi muodostaa lausekkeita, mutta harva käytti murto- ja desimaalilukuja samassa lausekkeessa. Tämä voi johtua oppilaiden ajatusmallista, jossa murto- ja desimaaliluvut ovat erillisiä, toisiinsa liittymättömiä matemaattisia käsitteitä. He eivät välttämättä hahmottaneet, että molempia voi käyttää samassa lausekkeessa, kuten 0,5 + 1/2 = 1. Koska murto- ja desimaalilukukäsitteet usein opetetaan erikseen, niiden rinnakkaisuus ei välttämättä sisäisty kaikille oppilaille.
Matematiikka-ahdistus yhteydessä heikompaan matematiikan osaamiseen jo ala-asteella
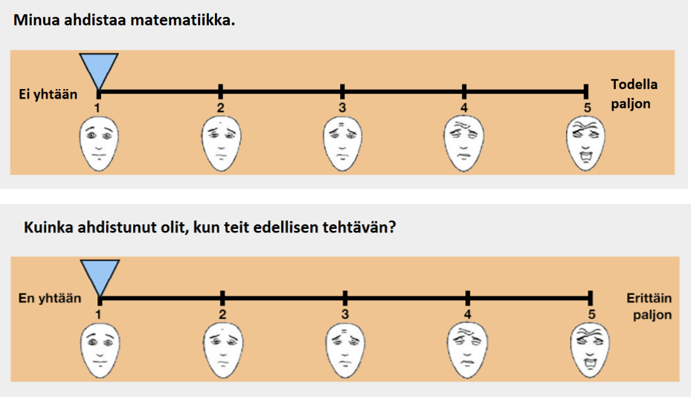
Tutkimuksessa selvitettiin myös 5. ja 6. luokkaisten oppilaiden matemaattisen osaamisen yhteyttä matematiikka-ahdistukseen monenlaisissa matemaattisissa tehtävissä (Halme et al., 2022). Tulosten mukaan 5. ja 6. luokkalaisten oppilaiden matematiikka-ahdistus on yhteydessä heikompaan kokonais- ja murtolukuosaamiseen, sekä joustavaan rationaalilukuosaamiseen. Tämän lisäksi tehtäväkohtainen matematiikka-ahdistus selitti heikompaa joustavaa rationaalilukuosaamista jopa silloin, kun muut mitatut matemaattiset taidot oli otettu huomioon. Tämä tarkoittaa sitä, että rationaalilukujen käyttäminen uudessa tehtävätyypissä tuotti ahdistusta joillekin oppilaille riippumatta heidän matemaattisen osaamisen tasosta. Matematiikka-ahdistus ei kuitenkaan näyttänyt liittyvän oppilaiden kykyyn huomata määrällisiä matemaattisia suhteita, kuten SFOR-tehtävässä. Tämän vuoksi tukemalla oppilaiden spontaania huomion kiinnittämistä määrällisiin suhteisiin voisi mahdollisesti vahvistaa murtolukuosaamista myös oppilailla, jotka kokevat matematiikka-ahdistusta.
Oppilaiden matemaattinen osaaminen kehittyy kuitenkin lukuvuoden aikana, erityisesti murtolukutehtävissä ja joustavassa rationaalilukuosaamisessa. Samalla oppilaiden tehtäväkohtainen matematiikka-ahdistus laskee. Yleisen matematiikka-ahdistuksen taso ei toisaalta muutu merkittävästi lukuvuoden aikana. Tämä kuvastaa sitä, että oppilaiden yleiseen matematiikka-ahdistukseen liittyy paljon muutakin kuin pelkästään tässä tutkimuksessa mitatut tehtävät. Tutkimuksesta selvisi myös, että matematiikka-ahdistus on yleisempää tytöillä kuin pojilla. Myös matemaattinen minäpystyvyys on heikompaa tytöillä. Matemaattiset taidot eivät kuitenkaan eronneet merkittävästi sukupuolten välillä.
Jos joustavan matematiikan osaamiseen liittyvät aiheet kiinnostavat sinua, voit löytää lisää tietoa Teknologiateollisuuden 100-vuotissäätiön opettajastipendeillä palkituista JoMa-täydennyskoulutuksista http://www.flexibility.fi. Kurssivalikoimasta löytyy esimerkiksi alakoulun opettajille suunnattu kurssi www.flexibility.fi/events/joustavat-aritmeettiset-taidot-alakoulussa/ (6 op) sekä kaikille perusopetuksen opettajille suunnattu kurssi www.flexibility.fi/events/matematiikan-oppimisvaikeudet/ (2 op) sekä joustavaa matemaattista ajattelua ja sen kehittämistä koskeva https://www.flexibility.fi/events/kohti-joustavaa-matemaattista-ajattelua/ . Tervetuloa mukaan!
Lähdeluettelo:
Braithwaite, D. W., Leib, E. R., Siegler, R. S., & McMullen, J. (2019). Individual differences in fraction arithmetic learning. Cognitive Psychology, 112, 81–98. https://doi.org/10.1016/j.cogpsych.2019.04.002
Dowker, A., Sarkar, A., & Looi, C. Y. (2016). Mathematics anxiety: What have we learned in 60 years? Frontiers in Psychology, 7, 1-16. https://doi.org/10.3389/fpsyg.2016.00508
Halme, H., Trezise, K., Hannula-Sormunen, M., & McMullen, J. (2022). Characterizing mathematics anxiety and its relation to performance in routine and adaptive tasks. Journal of Numerical Cognition, 8(3), 414-429. https://doi.org/10.5964/jnc.7675
McMullen, J., Hannula-Sormunen, M. M., & Lehtinen, E. (2014). Spontaneous Focusing on Quantitative Relations in the Development of Children’s Fraction Knowledge. Cognition and Instruction, 32(2), 198–218. https://doi.org/10.1080/07370008.2014.887085
McMullen, J., Hannula‐Sormunen, M. M., Lehtinen, E., & Siegler, R. S. (2022). Predicting adaptive expertise with rational number arithmetic. British Journal of Educational Psychology, 92(2), 1–19. https://doi.org/10.1111/bjep.12471
Määttä, S., Hannula-Sormunen, M., Halme, H., & McMullen, J. (2022). Guiding students’ attention towards multiplicative relations around them: A classroom intervention. Journal of Numerical Cognition, 8(1), 36–52. https://doi.org/10.5964/jnc.6363
Van Hoof, J., Verschaffel, L., & Van Dooren, W. (2015). Inappropriately applying natural number properties in rational number tasks: characterizing the development of the natural number bias through primary and secondary education. Educational Studies in Mathematics, 90(1), 39–56. https://doi.org/10.1007/s10649-015-9613-3

